Chacune des droites joignant l'un des sommets au milieu du côté opposé est une médiane
Tout triangle a trois médianes

|
Médiane Chacune des droites joignant l'un des sommets au milieu du côté opposé est une médiane Tout triangle a trois médianes |
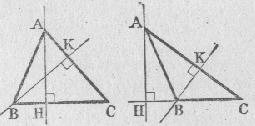
|
Hauteur Chacune des droites perpendiculaire à un côté et passant par le sommet opposé est une hauteur Tout triangle a trois hauteurs |
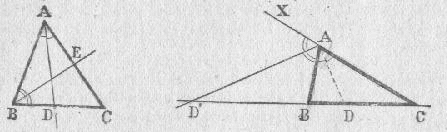
|
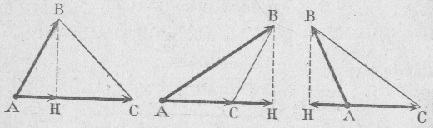
Bissectrice La bissectrice d'un angle coupe cet angle en deux angles égaux Le point d'intersection d'une bissectrice avec le côté opposé est appelé pied Une bissectrice peut être vue comme intérieure au triangle (par ex. angle BAC sur la figure de gauche) ou extérieure au triangle (par ex. angle BAX sur la figure de droite) Tout triangle a trois bissectrices intérieures et trois bissectrices extérieures |
|
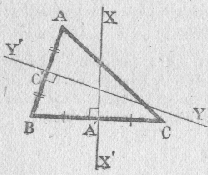
Médiatrice On appelle médiatrice d'un segment la droite perpendiculaire à ce segment en son milieu Tout triangle a trois médiatrices |
Particularité de ces différents droites
|
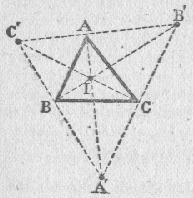
Les bissectrices intérieures sont concourantes en un point qui est le centre du cercle inscrit. La bissectrice intérieure d'un des angles et les bissectrices extérieures des deux autres angles sont concourantes |
|
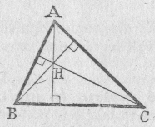
Les hauteurs sont concourantes en un point appelé orthocentre |

|
Les médianes sont concourantes en un point qui est le centre de gravité |
|
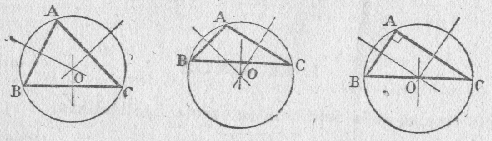
Les médiatrices sont concourantes en un point qui est le centre du cercle circonscrit au triangle |
|
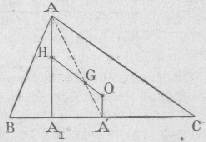
Le point de concours H des hauteurs, le point de concours G des médianes et le point de concours O
des médiatrices sont sur une même droite appelée droite d'Euler de plus, on a : OH = 3 . OG |
Relations dans le triangle
Relations dans un triangle rectangle
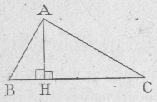
|
HB . CB = AB2 HC . BC = AC2 BH . AC2 = CH . AB2 HB . HC = HA2 AH . BC = AB . AC |
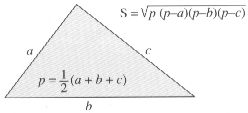
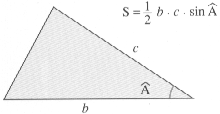
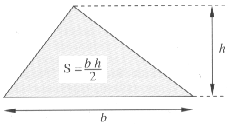
Relations dans un triangle quelconque
a = BC ; b = AC ; c = AB ; p = demi-périmètre ; hB = hauteur du sommet B ; mA = longueur de la médiane AM
Relations donnant la surface
 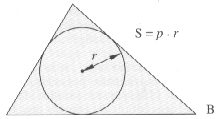
|
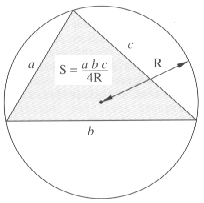
|
|
a2 = b2 + c2 - 2.b.c.cos A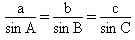 = Diamètre du cercle circonscrit = Diamètre du cercle circonscrit
|
|
hB = 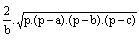 a2 = c2 + b2 + 2 . b . AH |
|
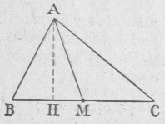
mA2 = 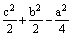 c2 + b2 = 2 . mA2 + a2 / 2 c2 - b2 = 2 . a . HM |
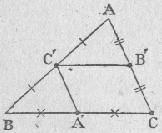
|
Le segment qui a pour extrémités les milieux de deux des côtés d'un triangle est parallèle au troisième et de longueur moitié |
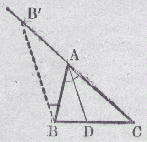
|
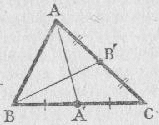
Soit D, le pied de la bissectrice intérieure de l'angle A d'un triangle quelconque ABC. On mène par le point B, la parallèle à cette bissectrice. Soit B', le point d'intersection entre cette parallèle et la droite AC. B'A / AC = BD / DC On a : . BB'A = DAC . DAC = BAD . BAD = ABB' et donc on a : BB'A = ABB', c'est à dire le triangle ABB' est isocèle, d'où AB' = AB. On en tire : DB / DC = AB / AC d'où : 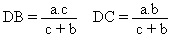
|
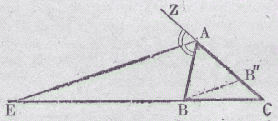
|
Soit E, le pied de la bissectrice extérieure de l'angle A d'un triangle quelconque ABC. On mène par le point B, la parallèle à cette bissectrice. Soit B", le point d'intersection entre cette parallèle et la droite AC. EB / EC = AB" / AC On a : . B"BA = EAB . EAB = EAZ . ZAE = AB"B et donc on a : B"BA = AB"B, c'est à dire le triangle ABB" est isocèle, d'où AB" = AB. On en tire : EB / EC = AB / AC d'où : 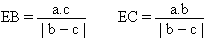
|