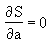
et
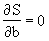
soit
Rechercher une régression entre des coordonnéees de points donnés correspond à trouver l'équation d'une courbe dont on se donne la forme, et qui s'approche le plus possible de tous les points donnés.
Dans le cas où l'on souhaite que la courbe cherchée passe par les points donnés, la regression devient une interpolation.
| y = a.x + b | y = a . eb.x | y = a . xb | y = a.x2 + b.x + c |
La technique principale de recherche des coefficients a et b consiste à se dire
que l'on souhaite que la somme des erreurs entre les valeurs évaluées par la régression et les
valeurs réelles soit la plus faible possible.
En fait, on cherchera à minimiser la somme des carrés de ses erreurs, d'où le nom de
droite des moindres carrés.
Explications pour un calcul dans l'espace :
Soit N points Mi donnés de coordonnées ( Xi , Yi ) ( i = 1 à N )
Pour chaque point, la valeur évaluée pour l'abcisse Xi sera Y*i
L'erreur pour le point M i sera donc |Yi-Y*i|
La somme des carrés des erreurs est S = S (Yi-Y*i)2
or Y*i = a.Xi + b
d'où
S = S [Yi-(a.Xi + b)]2
On développe le carré
S = S ( Yi2 - 2.b.Yi + b2 + a2.Xi2 + 2.a.b.Xi - 2.a.Xi.Yi )
On développe la somme
S = S Yi2 - 2.b.S Yi + S b2 + a2.S Xi2 + 2.a.b.S Xi - 2.a.S Xi.Yi
soit
S = S Yi2 - 2.b.S Yi + N.b2 + a2.S Xi2 + 2.a.b.S Xi - 2.a.S Xi.Yi
Les valeurs de a et b sont telles que S est minimal
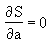
et
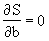
soit
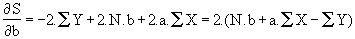
d'où
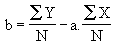
on remarquera que le barycentre des points M est situé sur la droite de régression
on reporte la valeur de b dans l'équation de S
on arrive après developpement puis regroupement à :

ce qui mène à

et donc

Il suffit ici de faire un chagement de variable.
En effet, si on prend le logarithme de part et d'autre de l'expression y = a.eb.x
ln(y) = ln(a) + b.x
Posons Y=ln(y), X=x, A=b, B=ln(a)
On abouti à l'équation Y = A.X + B
dont on trouve les coefficients A et B suivant la méthode décrite dans le paragraphe ci-dessus.
On revient aux coefficients a et b par
a = eB
et
b = A
Il suffit ici de faire un chagement de variable.
En effet, si on prend le logarithme de part et d'autre de l'expression y = a.xb
ln(y) = ln(a) + b.ln(x)
Posons Y=ln(y), X=ln(x), A=b, B=ln(a)
On abouti à l'équation Y = A.X + B
dont on trouve les coefficients A et B suivant la méthode décrite dans le paragraphe ci-dessus.
On revient aux coefficients a et b par
a = eB
et
b = A
On cherche à touver les coefficients a, b et c tels que la somme des erreurs soit minimale.
S = S [Yi-(a.Xi2 + b.Xi + c)]2
Les 3 dérivées partielles sont nulles et permettent d'établir un systême de 3 équations avec les 3 inconnues a, b et c
Passons les différentes étapes.
On abouti à :
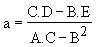 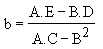  |
avec |
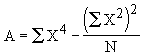 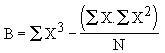 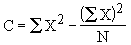 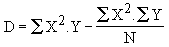 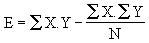 |