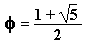
Comment obtenir le nombre d'or par le calcul
Division d'un segment de droite en moyenne et extrême raison
Décagones réguliers convexe et étoilé
Pentagones réguliers convexe et étoilé
Figure regroupant les pentagones et décagones convexes et étoilés
Méthodes de construction d'un pentagone
Les différents types de rectangles liés au nombre d'or
Comment tracer un rectangle de forme A
Spirales logarithmiques construites à partir de rectangles
Triangles liés au nombre d'or
Spirale logarithmique construite à partir de triangles d'or
Pavage de Penrose
Chryzode
Barrage triangulaire
Coquillages
Paon faisant la roue
Fleur de tournesol
Implantation de feuilles sur une tige
Le nombre d'or, appelé aussi divine proportion est un nombre irrationnel que l'on rencontre en mathématiques dans nombre de disciplines.
On le retrouve aussi dans la nature (dans la façon qu'ont les feuilles à se disposer sur une tige),
en musique, en peinture (contenant ou contenu d'un tableau), en architecture...
Il semble qu'il est été connu bien avant les grecs.
Comment obtenir le nombre d'or par le calcul :
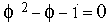 |
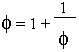 |
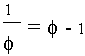 |
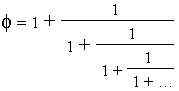
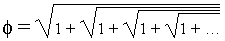
Soit Un telle que Un+2 = Un+1 + Un
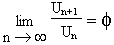
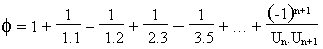
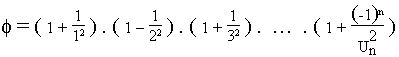
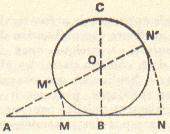
Division d'un segment de droite en moyenne et extrême raison
|
Soit le segment de droite [AB]. On cherche un point M de (AB) tel que AM2 = AB . MB On peut remarquer tout de suite que si la longueur AB est prise pour unité, et si on prend le point A comme origine des distances, l'expression ci-dessus peut s'écrire x 2 = 1 . (1-x) soit 1/(1/x)2 = 1 - 1 / (1/x) d'où on tire 1/x = 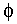 . .On aura donc 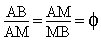
Construction du point M' : 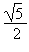 . AB . AB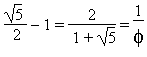 . AB . AB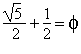 . AB . ABOn a finalement : 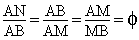
|
Décagones réguliers convexe et étoilé
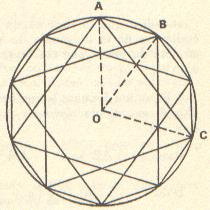
|
Soient le décagone convexe de côté AB et le décagone étoilé de côté AC On a : 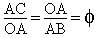
L'angle AOB est de 36°.
L'angle OAC est de 36° AC = 2 . OA . cos 36°, soit AC/OA = 2.cos 36° d'où
|
Pentagones réguliers convexe et étoilé
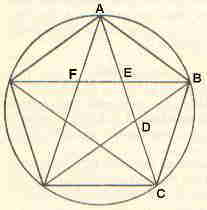
|
AB = AD BD = DF 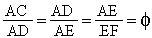
|
Figure regroupant les pentagones et décagones convexes et étoilés
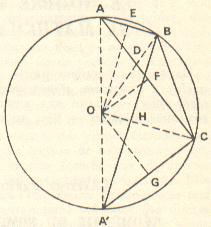
|
Dans la figure ci-contre sont représentés :
On a : 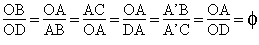
|
Méthodes de construction d'un pentagone
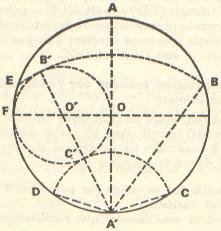
|
Tracer le cercle de centre O' et de rayon moitié de celui du cercle circonscrit Tracer les arcs de cercle de centre A' et tangents au cercle de centre O' Ces arcs de cercle coupent le cercle circonscrit aux points B, C, D et E, qui forment un pentagone avec le point A |
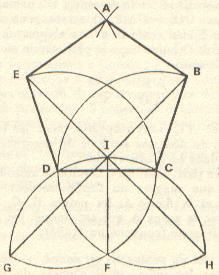
|
Tracer le cercle de centre C et passant par D et le cercle de centre D et passant par C Ces deux cercles se coupent en F Tracer la bissectrice FI du segment CD Tracer le cercle de centre F et passant par C et D Ce cercle coupe la droite FI en I et les cercles précédents en G et H Tracer les droites GI et HI Ces droites coupent les cercles en B et E |
Les différents types de rectangles liés au nombre d'or
| forme A |  |
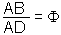 |
|
| forme B | 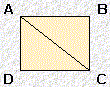 |
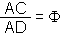 |
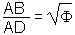 |
| forme C | 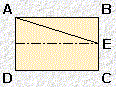 |
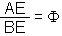 |
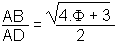 |
| forme D | 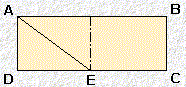 |
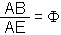 |
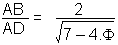 |
| forme E | 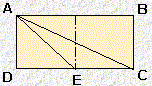 |
 |
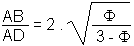 |
| forme F | 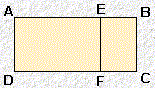 |
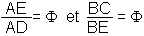 |
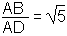 |
| forme G | 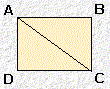 |
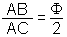 |
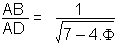 |
| forme H |  |
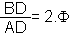 |
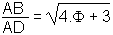 |
| forme I |  |
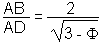 |
|
| forme J | 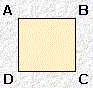 |
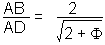 |
|
| forme K | 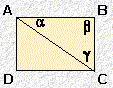 |
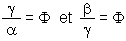 |
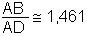 |
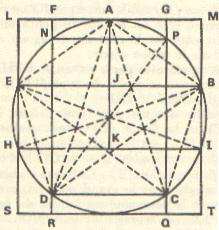
Dans la figure suivante, on retrouve différentes formes :
|
Forme C : rectangles GCDF, JEHK, JBIK
Forme D : rectangle LMBE Forme G : rectangles PCDN, ALEJ, AMBJ Forme H : rectangle EBIH Forme I : rectangle GQRF Forme J : rectangle MTSL |
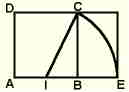
Comment tracer un rectangle de forme A :
|
Soit AD = 1 AB = 1 AI = IB = 1/2 BC = 1 IC² = IB² + BC² soit IC = 5/4 IE = IC AE = AI + IE = F
Remarque :
Si on onlève le plus grand carré possible d'un rectangle de forme A, |
Spirales logarithmiques construites à partir de rectangles :
|
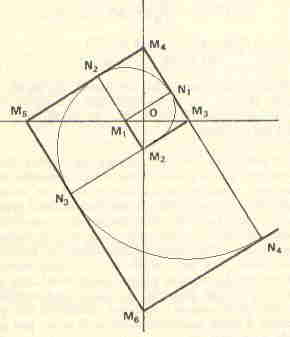
Dans la figure ci-contre, on note : - différents rectangles de forme A - Les axes tracés sont tels qu'ils passent par 3 sommets de chacun des rectangles
Les segments OM1, OM2,OM3,OM4,OM5,OM6
|
|
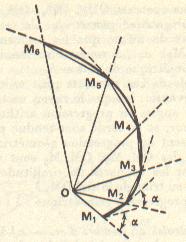
Une spirale logarithmique est telle que : -lorsque l'on fait tourner le rayon vecteur OMn d'un angle constant, la longueur OMn et la longueur Mn-1Mn suivent une progression géométrique -l'angle entre un rayon vecteur OMn et la tangente en Mn est une constante |
|
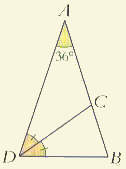
Le triangle ABD est tel que : - angle A = 36° - angle B = angle D = 72°
on démontre que AB / BD = F
la bissectrice de l'angle D coupe AB en C |
Spirale logarithmique construite à partir de triangles d'or
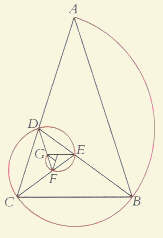
|
Si on joint les sommets de triangles d'or construits suivant la méthode décrite ci-dessus, on obtient une spirale logarithmique |
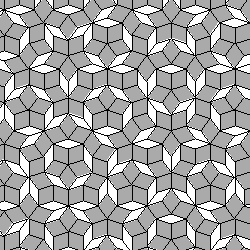 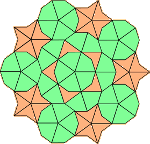
|
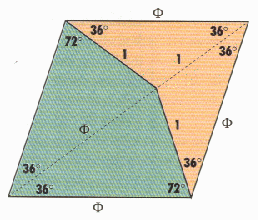
Ces pavages sont composés de deux formes composées : ( voir la figure ci-dessus pour l'appelation des points ) - 2 triangles d'or type BCD accolés pour la forme blanche/verte - 2 triangles d'or type ABD accolés pour la forme grise/orange |
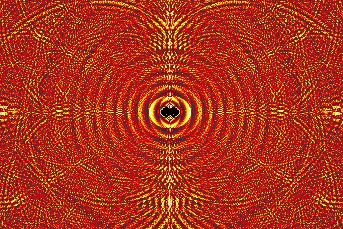
|
Ce dessin, appelé chryzode est une des multiples figures se rapportant au nombre d'or. |
|
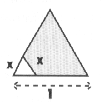
Soit un barrage dont la section est un triangle équilatéral de longueur unité Si on tronque ce triangle parallèlement à une des faces, d'une longueur x, le barrage basculera pour une certaine longueur x Les calculs montrent que x = 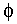
|

|
La croissance d'un coquillage se fait selon une suite géométrique. La forme du coquillage ci-contre ( une ammonite ) est une spirale logarithmique. De même, les différentes cloisons délimitent des surfaces suivant une progression géométrique. |

|
Les "yeux" des plumes de paon sont disposés selon des spirales logarithmiques |

|
L'étude de la disposition des graines de tournesol montrent qu'elles sont
disposées selon des spirales logarithmiques nommées parastiches. Il en est de même pour l'implantation des écailles sur une pomme de pin ou un ananas... Les parastiches sont enroulées dans le sens horaire et dans le sens anti-horaire. Si on compte le nombre de parastiches pour chaque sens, on trouve : 5 et 8 pour les écailles de pomme de pin; 8 et 13 pour les écailles de l'ananas; 34 et 55 pour les graines de tournesol... or ces différents nombres appartiennent à la suite de Fibonacci. La différence du nombre de parastiches entre les différentes espèces provient de la vitesse de pousse de la plante. L'angle au centre entre une graine et celle née avant elle est une constante ,et vaut 137.5°. Cet angle est l'angle appelé angle d'or, et vaut 360°/(1+F) |
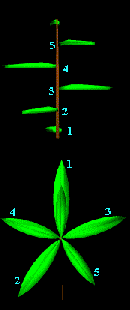
Implantation de feuilles sur une tige
|
Il existe un certain nombre de d'espèces de fleurs et d'arbres ( poirier, pommier, chêne ..)
pour lesquels les feuilles sont disposées selon 5 génératrices autour de la tige.
Les feuilles sont disposées selon une hélice qui s'enroule autour de la tige.
Si partant d'une feuille quelconque, on décrit l'hélice, il faut décrire 2 spires pour
retomber à l'horizontal de la feuille de départ. La rapport 2 (nombre de spires) / 5 (nombre de feuilles par spire) est appelé cycle foliaire. On constate que le nombre inverse du cycle foliaire appartient toujours à une suite dont la limite est f2. |