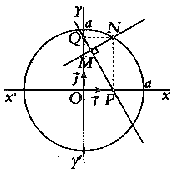
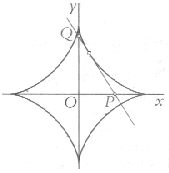
Ce point se projette en P sur x'x et en Q sur y'y.
Soit M, le projeté orthogonal de N sur (PQ).
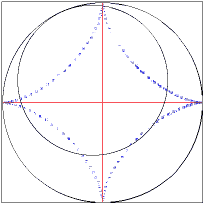
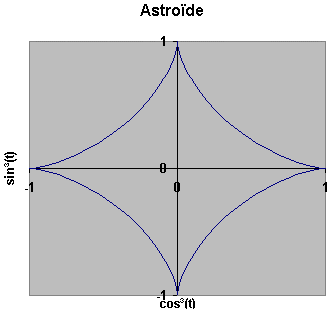
La trajectoire décrite par le point M est une astroïde
Astroïde
autres noms : cubocycloïde, paracycle, courbe à 4 cornes
Méthode 1
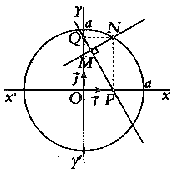
|
Soit un point N décrivant le cercle de centre O et de rayon a. Ce point se projette en P sur x'x et en Q sur y'y. Soit M, le projeté orthogonal de N sur (PQ). La trajectoire décrite par le point M est une astroïde |
|
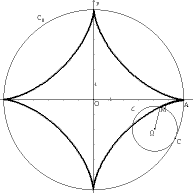
L'astroïde est la courbe décrite par un point M d'un cercle de rayon r roulant sans glisser à l'intérieur d'un cercle de rayon 4r. L'astroïde est donc une hypocycloïde. |
|
L'astroïde est la courbe décrite par un point M d'un cercle de rayon 3r roulant sans glisser à l'intérieur d'un cercle de rayon 4r. L'astroïde est donc une hypocycloïde. |
|
Soit un segment PQ de longueur a, et tel que le point P est sur l'axe x'x
et le point Q est sur l'axe y'y. On fait glisser le point P le long de l'axe P'P. On fait de même pour les quatre quadrants du plan. L'enveloppe des différentes positions de PQ ast une astroïde |
|
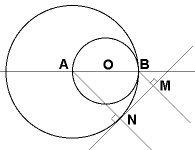
Soit le cercle C de centre O et de diamètre 2r. Soit le cercle C ' de centre A et de rayon 2r. Soit un point N décrivant le cercle C '. Le point M est l'intersection de la tangente au cercle C ' passant par N et de la droite parallèle au rayon AN et passant par B. Le point M décrit une astroïde. |
|
Equation cartésienne :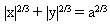 ou (x2+y2-a2)3 + 27.a2.x2.y2 = 0
Equation paramétrique :
Equation polaire :
Longueur de la courbe = 6.a |