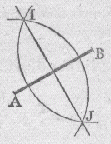
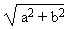
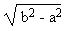
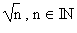
1) Construire la médiatrice d'un segment donné

Dessiner deux arcs de cercle de centre respectif A et B, et ayant un même rayon assez grand pour qu'ils se coupent. Les points communs I et J font partie de la droite médiatrice.

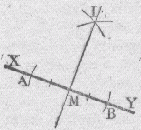
2) Construire la perpendiculaire à une droite donnée XY en un point donné M de cette droite

A l'aide du compas pointé en M, tracer les points A et B équidistants du point M (distance quelconque). La droite perpendiculaire cherchée est la médiatrice du segment AB, et on peut la tracer suivant la méthode décrite en 1.

3) Construire une droite perpendiculaire à une droite donnée XY et passant par un point donné

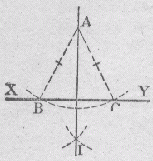
Tracer un arc de cercle de centre A et coupant la droite XY en deux points assez distants, notés B et C. La droite perpendiculaire cherchée est la médiatrice du segment BC, et on peut la tracer suivant la méthode décrite en 1.

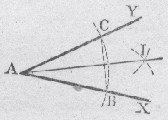
4) Construire sans rapporteur la bissectrice d'un angle donné

Tracé un arc de cercle de centre A et coupant les côtés de l'angle donné en deux points, notés B et C. La bissectrice recherchée est tracée suivant la méthode décrite en 3 (médiatrice du segment BC passant par A)

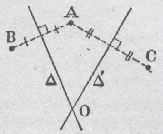
5) Rechercher le point équidistant de trois points donnés
en d'autres termes : Rechercher le centre du cercle dont font partie 3 points donnés

Le point O recherché correspond à l'intersection des médiatrices D et D' des segments AB et AC.

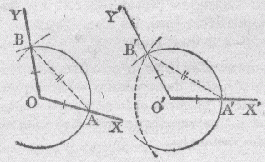
6) Construire sans rapporteur un angle égal à un angle donné

Tracer le côté O'X' de l'angle. Tracer un arc de cercle de centre O et coupant les côtés de l'angle à dupliquer en A et B. Tracer le cercle de centre O' et de même rayon OA. Ce cercle coupe le côté O'X' en A'. A l'aide du compas, prendre la longueur AB et tracer un arc de cercle de centre A' et de rayon égal à l'ouverture du compas. Cet arc de cercle coupe le cercle de centre O' au point B'. Tracer le côté O'Y' passant par B'.

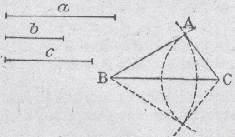
7) Construire un triangle ayant ses trois côtés respectivement égaux à trois segments donnés

Tracer l'un de ses côtés, par exemple le côté BC égal à a. Tracer le cercle de centre B et de rayon c. Tracer le cercle de centre C et de rayon b. Si les deux cercles se coupent, les points communs forment le triangle recherché avec les poinrs B et C. Il faut que chaque segment est une longueur comprise entre la différence et la somme de celle des deux autres.

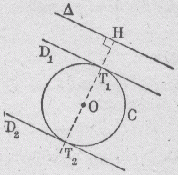
8) Mener à un cercle donné des tangentes parallèles à une droite donnée.

Tracer la perpendiculaire OH à la droite D et passant par le centre O du cercle C. Les points de rencontre de cette droite avec le cercle C sont les points de contact T1 et T2 des tangentes recherchées. Tracer alors les tangentes D1 et D2, perpendiculaires à OH aux points T1 et T2.

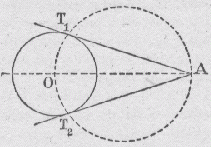
9) Mener à un cercle donné, des tangentes passant par un point donné.

Tracer le cercle de diamètre OA. Les points d'intersection de ce cercle avec le cercle C sont les points de contact des tangentes. Tracer les droites AT1 et AT2.

10) Mener des tangentes communes à deux droites données.

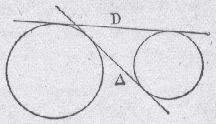
La droite D est une tangente commune extérieure. La droite D est une tangente commune intérieure.

10a) Construction des tangentes communes extérieures à deux cercles données

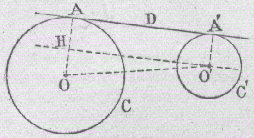
Etude du problème. On suppose que l'on a trouvé une tangente commune extérieure D. Soient A et A' les points de contact avec les cercles C et C'. Soit H, le point d'intersection du rayon OA avec la parallèle à la droite D passant par O. on a : OH = OA - HA = R - R' La droite OH, perpendiculaire à OA, est en fait une tangente au cercle de centre O et de rayon R-R'. Les tangentes communes extérieures aux deux cercles donnés sont parallèles aux tangentes menées du point O' au cercle de centre O et de rayon R-R'.

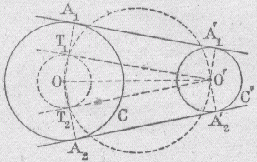
Réalisation de la construction Tracer le cercle de centre O et de rayon R-R'. Tracer les tangentes à ce cercle et passant par le point O'. (voir 9) Prolonger les rayons OT1 et OT2, qui coupent le cercle C aux points A1 et A2. Les tangentes communes recherchées sont les parallèles menées respectivement des points A1 et A2 aux droites O'T1 et O'T2.

10b) Construction des tangentes communes intérieures à deux cercles donnés.

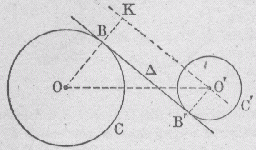
	Etude du problème. On suppose que l'on a trouvé une tangente commune intérieure D. Soient B et B' ses points de contact. Soit K le point d'intersection entre le rayon OB et la parallèle à D passant par O'. On a : OK = OB + BK = R + R' Les tangentes communes intérieures sont parallèles aux tangentes menées du points O' au cercle de centre O et de rayon R+R'.
	Réalisation de la construction. Tracer le cercle de centre O et de rayon R+R'. Tracer les tangentes O'S1 et O'S2 à ce cercle passant par le point O'. (voir 9) Soient B1 et B2 les points d'intersection des droites OS1 et OS2 avec le cercle C. Les tangentes communes recherchées sont les parallèles menées respectivement des points B1 et B2 aux droites O'S1 et O'S2.

11) Construire un triangle connaissant deux côtés et l'angle opposé à l'un d'eux

11a) L'angle est aigu

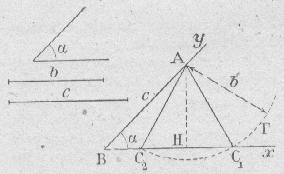
Construire un angle xBy égal à l'angle donné (voir méthode 6). Sur l'un des côtés (par exemple By) de cet angle, on porte une longueur BA égale à c. Le point C doit être situé sur la demi-droite Bx et être situé à une distance b du point A. Le point C est donc l'intersection de la demi-droite Bx avec le cercle G de centre A et de rayon b. Soit H, le pied de la perpendiculaire à Bx passant par A. * si AH < b < c, il existe deux points C1 et C2 et donc deux triangles. * si b < AH, il n'y a pas de point d'intersection et donc pas de triangle répondant à la question. * si b ³ c, il n'y a qu'un point commun, et donc un seul triangle.

11b) L'angle est obtus

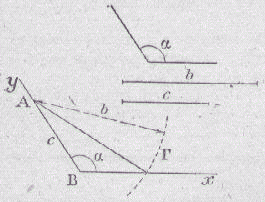
Construire un angle xBy égal à l'angle donné (voir méthode 6). Sur l'un des côtés (par exemple By) de cet angle, on porte une longueur BA égale à c. Le point C doit être situé sur la demi-droite Bx et être situé à une distance b du point A. Le point C est donc l'intersection de la demi-droite Bx avec le cercle G de centre A et de rayon b. * si b > c, il n'y a qu'un point commun, et donc un seul triangle. * si b £ c, il n'y a pas de point d'intersection, et donc pas de triangle répondant à la question

12) Construire un triangle rectangle connaissant l'hypothénuse et la hauteur correspondante

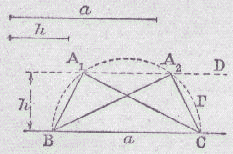
Tracer le segment BC égal à a. Le triangle étant rectangle, le point A appartient au cercle G ayant BC comme diamètre. D'autre part, le point A doit être à la distance h de la droite BC, et appartient donc à la droite D parallèle à BC située à la distance h de BC. (une droite de part et d'autre de BC) * si 2.h < a, il existe 4 points communs, et il y a donc quatre triangles possibles, tous égaux. * si 2.h = a, il existe 2 points communs, et il y a donc deux triangles possibles, isocéles en A. * si 2.h > a, il n'existe pas de point commun, et il n'y a pas de triangle possible.

13) Construire un triangle connaissant le rayon du cercle inscrit, un angle et l'une des hauteurs

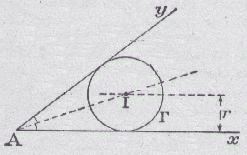
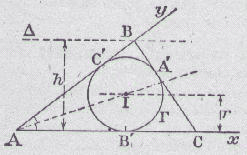
Tracer un angle xAy égal à l'angle donné. Le centre I du cercle inscrit G au triangle à trouver est tel que : * I est situé sur la bissectrice de yAx * I est situé à la distance r (donnée) de la droite Ax

premier cas : la hauteur donnée est celle issue de B ou de C

On suppose sur la figure ci-contre que la hauteur donnée est celle issue de B. Le point B se trouve à la distance h de la droite Ax et donc appartient à la parallèle D à Ax située à la distance h de Ax. Le point B est le point d'intersection de la droite D et de la droite Ay. Le côté BC est tangent au cercle G et on le tracera suivant la méthode décrite en 9. Pour que le problème soit résoluble, il faut h > 2.r

deuxième cas : la hauteur donnée est celle issue de A

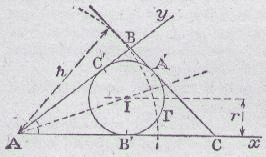
La droite BC, devant passer à la distance h du point A, doit être tangente au cercle de centre A et de rayon h. D'autre part, la droite BC doit être tangente au cercle G. La droite BC est donc une tangente commune extérieure à ces deux cercles, et on la tracera suivant la méthode décrite en 10a. Pour que le problème soit résoluble, il faut : - qu'il soit possible de mener une tangente commune extérieure aux deux cercles et donc que h £ AI + r - que le cercle G soit inscrit est donc que h > 2.r

14) Relation entre les cordes d'un cercle, portées par deux droites qui se coupent

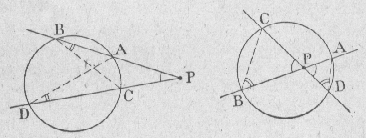
14a) les deux droites coupent le cercle

PA . PB = PC . PD

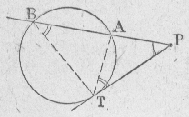
14b) l'une des droites est sécante et l'autre tangente

PT2 = PA . PB

14c) Puissance d'un point P par rapport à un cercle C

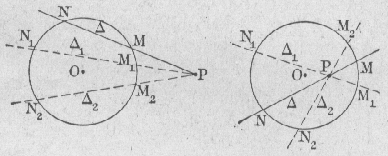
si on pivote autour du point P, le produit PM.PN reste constant. Cette constante est appelée puissance du point P par rapport au cercle C. Soit d, la distance du point P au centre du cercle Soit R, le rayon du cercle Soit p, la puissance du point P par rapport au cercle C On a : p = d2 - R2

15) Construction de la longueur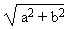

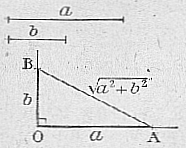
Il suffit de construire un triangle rectangle dont les côtés de l'angle droit soient respectivement égaux aux deux segment donnés

16) Construction de la longueur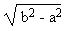

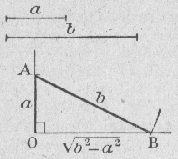
On construit un triangle rectangle ayant un côté de l'angle droit égal à a et l'hypothénuse égale à b. Le deuxième côté de l'angle droit est le segment cherché

17) Construction de la moyenne géométrique de deux longueurs données

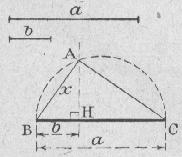
	méthode 1: Tracer sur une même droite, de manière qu'ils empiètent l'un sur l'autre, deux segments respectivement égaux à a et b On obtient les points B, C et H. Tracer le cercle de diamètre a. Tracer la perpendiculaire à BC passant par H. Le point d'intersection entre cette perpendiculaire et le cercle donne le point A. Dans le triangle ABC, rectangle en A, on a : BH . BC = AB2
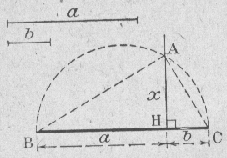
	méthode 2 : Porter sur une même droite, à la suite l'un de l'autre, deux segments BH et HB respectivement égaux à a et b. Tracer le cercle de diamètre BC. Tracer la perpendiculaire à BC passant par H. Le point d'intersection entre cette perpendiculaire et le cercle donne le point A. Dans le triangle ABC, rectangle en A, on a : BH . HC = AH2
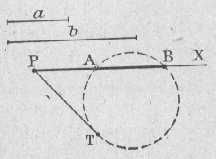
	méthode 3 : Tracer sur une même droite, de manière qu'ils empiètent l'un sur l'autre, deux segments respectivement égaux à a et b On obtient les points P, A et B. Tracer un cercle passant par les points A et B. Tracer une tangente à ce cercle passant par le point P. On a : PA . PB = PT2

18) Construction de deux longueurs dont on connait la somme et la moyenne géométrique

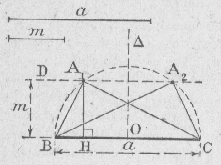
Comparer à la construction 172. Soit x = BH et y = HC On a : * x + y = BC = a * x . y = AH2 Construction : Tracer un cercle de diamètre BC = a Tracer la parallèle D au diamètre BC, située à la distance m de ce diamètre Les points d'intersection sont les points A1 et A2 Tracer la hauteur AH, qui découpe le diamètre BC en deux longueurs BH et HC qui sont les longueurs cherchées Si a > 2.m, il y a deux points A de part et d'autre de BC, pour deux solutions possibles Si a = 2.m, il y a un point A de part et d'autre de BC, pour une seule solutions Si a < 2.m, il n'y a pas de point A et donc pas de solution

19) Construction de deux longueurs dont on connait la différence et la moyenne géométrique

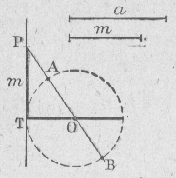
Tracer un cercle de diamètre a Mener une tangente quelconque à ce cercle, et à partir du point de contact T, prendre une longueur PT = m Tracer la droite passant par P et par le centre du cercle, qui coupe ce cercle aux points A et B On a : * PB - PA = a * PA . PB = PT2 = m2 Les longueurs PA et PB sont donc les longueurs cherchées

20) Construction de la longueur

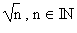
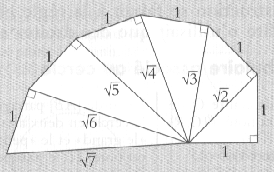
Tracer un triangle rectangle isocèle unitaire. Tracer successivement les triangles rectangles jusqu'à la longueur recherchée

21) Construction de la longueur aⁿ

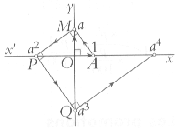
Tracer 2 axes orthonormés x'x et y'y. Tracer OA=1 et OM=a. La perpendiculaire en M à (AM) coupe x'x en P tel que OP=a2. Tracer successivement les perpendiculaires jusqu'à obtenir an.

22) Construction d'un carré dont on connait la différence entre la diagonale et le côté

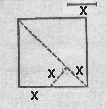
Tracer un angle droit et sa bissectrice. Reporter sur la bissectrice la longueur donnée. A partir du point d'arrivée, reporter la longueur donnée vers l'un des côtés de l'angle droit. A partir du point d'arrivée, reporter la longueur donnée sur le côté de l'angle droit.